Question

Four charges are located at the corners of a square. Each side of the square is 37 m. The left two charges have a positive charge of 20 micro-Coulombs. The right two charges have a negative charge of 22 micro-Coulombs. What is the magnitude of the electric field at the center of the square?

Answer 1

E = 781.12 N/C

Step-by-step explanation:

Look at the attached graphic:

The 20µC charges are positive , then, the electric fields leave the charge.

The 22µC charges are negative, then, the electric fields enter the charge.

The electric field due to each of the charges is calculated by Coulomb's law:

E= k*q/d²

E: Electric field in N/C

q: charge in Newtons (N)

k: electric constant in N*m²/C²

d: distance from charge q to point P in meters (m)

Problem development

The electric field at a point P due to several point charges is the vector sum of the electric field due to individual charges.

E₁, E₂, E₃, E₄: Electric field at point P due to charge q₁, q₂, q₃, and q₄ respectively

The electric field in the direction of the y axis at the point P in the center of the square is equal to zero because the sum of the vertical components upwards is equal to the sum of the vertical components downwards.

Calculation of the electric field in the direction of the x-axis in the center of the square (point P)

Eₓ = E₁ₓ + E₂ₓ + E₃ₓ + E₄ₓ

`d  = √(18.5^2+ 18.5^2)  =26.16m`

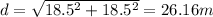
E₁ₓ = E₂ₓ = (9*10⁹)*(20*10⁻⁶)*cos(45°)/(d²) = (9*10⁹)*(20*10⁻⁶)*cos(45°)/(26.16²) = 185.98 N/C

E₃ₓ = E₄ₓ = (9*10⁹)*(22*10⁻⁶)*cos(45°)/(d²) = (9*10⁹)*(22*10⁻⁶)*cos(45°)/(26.16²) = 204.58 N/C

Eₓ = E = 2*185.98 +2*204.58 = 781.12 N/C