Answer : 745 K high you can raise the temperature of the gas without bursting the vessel.
Explanation :
Gay-Lussac's Law : It is defined as the pressure of the gas is directly proportional to the temperature of the gas at constant volume and number of moles.
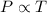
or,

where,
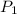 = initial pressure of gas = 0.800 atm
= initial pressure of gas = 0.800 atm
 = final pressure of gas = 2.00 atm
= final pressure of gas = 2.00 atm
 = initial temperature of gas =
= initial temperature of gas =
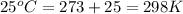
 = final temperature of gas = ?
= final temperature of gas = ?
Now put all the given values in the above equation, we get:
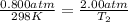
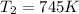
Therefore, the final temperature of the gas is 745 K