Question

A 2.04 g lead weight, initially at 10.8 oC, is submerged in 7.74 g of water at 52.2 oC in an insulated container. clead = 0.128 J/goC; cwater = 4.18 J/goC. What is the final temperature of both the weight and the water at thermal equilibrium?

Answer 1

Step-by-step explanation:

Hello, in this case, the lead is catching heat and the water losing it, that's why the heat relation ship is (D is for Δ):

`DH_(lead)=-DH_(water)`

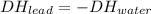
Now, by stating the heat capacity definition:

`m_(Pb)C_(Pb)*(T_(eq)-T_(lead)=-m_(H_2O)C_(H_2O)*(T_(eq)-T_(H_2O))\\`

Solving for the equilibrium temperature:

`T_(eq)=(m_(Pb)C_(Pb)T_(Pb)+m_(H_2O)C_(H_2O)T_(H_2O))/(m_(Pb)C_(Pb)+m_(H_2O)C_(H_2O)) \\\\T_(eq)=(2.04g*0.128J/(g^oC)*10.8^oC+7.74g*4.18J/(g^oC)*52.2^oC)/(2.04g*0.128J/(g^oC)+7.74g*4.18J/(g^oC)) \\\\T_(eq)=51.87^oC`

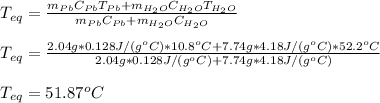
Which is very close to the water's temperature since the lead's both mass and head capacity are lower than those for water.

Best regards.