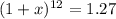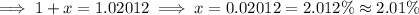Question

The number of users on a website is 1500 and is growing exponentially at a rate of 27% per year. Write a function to represent the number of users on the website after tt years, where the monthly rate of change can be found from a constant in the function. Round all coefficients in the function to four decimal places. Also, determine the percentage rate of change per month, to the nearest hundredth of a percent.

Answer 1

`A=1500(1+0.27)^t`

Rate of change per month would be 2.01%

Explanation:

Since, the exponential growth function,

`A=P(1+(r)/(n))^(nt)`

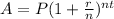
Where,

P = principal amount,

r = annual rate,

n = number of compounding periods,

t = number of years,

Here,

P = 1500, r = 27% = 0.27, n = 1,

Thus, the number of users after t years,

`A=1500(1+0.27)^t`

Let it is equivalent to number of users when it is growing at the rate of x monthly,

That is,

`1500(1+0.27)^t=1500(1+x)^(12t)`

`1.27^t=((1+x)^(12))^t`

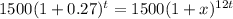
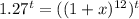
By comparing,

`(1+x)^(12)=1.27`

`\implies 1 + x = 1.02012\implies x = 0.02012=2.012\%\approx 2.01\%`