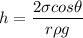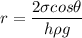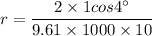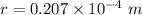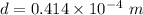Question

A capillary tube is immersed vertically in a water container. Knowing that water starts to evaporate when the pressure drops below 4 kPa, determine the maximum capillary rise and tube diameter for this maximum-rise case. Take the contact angle at the inner wall of the tube to be 6° and the surface tension to be 1.00 N/m.

Answer 1

`d=0.414* 10^(-4)\ m`

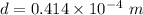
Step-by-step explanation:

Given that

P = 4 KPa

Contact angle = 6°

Surface tension = 1 N/m

Lets assume that atmospheric pressure = 100 KPa

Lets take that density of water =
`1000\ kg/m^3`

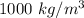
So the capillarity rise h

`h=(\Delta P)/(\rho g)`

`h=(100* 1000-4* 1000)/(1000* 10)`

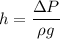
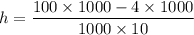
h= 9.61 m

We know that for capillarity rise h

`h=(2\sigma cos\theta )/(r\rho g)`

`r=(2\sigma cos\theta )/(h\rho g)`

`r=(2* 1 cos4^(\circ) )/(9.61* 1000* 10)`

`r=0.207* 10^(-4)\ m`

`d=0.414* 10^(-4)\ m`