Answer:
First equation remains same and second equation is divided by 2.
Explanation:
The given system of equations is

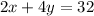
The new system of equation is

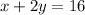
On comparing both system of equation we get that first equation of both systems are same.
If a we divide the second equation of original system of equations, then we get the second equation of new system of equations.
Second equation is
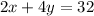
Divide both sides by 2.

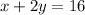
Therefore, we need to divide the second equation by 2, to create this new equivalent system of equations.