Question

A 2.0 g metal cube and a 4.0 g metal cube are 6.0 cm apart, measured between their centers, on a horizontal surface. For both, the coefficient of static friction is 0.65. Both cubes, initially neutral, are charged at a rate of 7.0 nC/s .

(a) Which cube moves first?

(b) How long after charging begins does one cube begin to slide away?

Answer 1

(a). The 2.0 g metal cube move fast than the 4 g metal cube.

(b). The time taken is 10.19 sec.

Step-by-step explanation:

Given that,

Mass of metal cube = 2.0 g

Mass of second metal cube = 4.0 g

Coefficient of static friction = 0.65

Charging rate = 7.0 nC/s

Distance = 6.0 cm

(a). We need to calculate the frictional force for 2.0 g metal cube

Using formula of frictional force

`F_(1)=\mu\ mg`

Put the value into the formula

`F_(1)=0.65*2.0*10^(-3)*9.8`

`F_(1)=12.74*10^(-3)\ N`

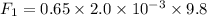
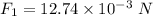
The frictional force for 4.0 g metal cube

`F_(2)=0.65*4.0*10^(-3)*9.8`

`F_(2)=25.48*10^(-3)\ N`

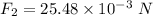
The motion of the cube is less when the friction is more.

The 2.0 g metal cube is having less frictional force.

Therefore, the 2.0 g metal cube move fast than the 4 g metal cube.

(b). We need to calculate the time

Firstly we need to calculate the charge

Using electrostatic force and frictional force

`F=\mu\ mg`

`(kq^2)/(r^2)=12.74*10^(-3)`

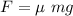
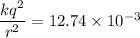
Put the value into the formula

`9*10^(9)*(q^2)/((6.0*10^(-2))^2)=12.74*10^(-3)`

`q^2=(12.74*10^(-3)*(6.0*10^(-2))^2)/(9*10^(9))`

`q^2=\sqrt{5.096*10^(-15)}`

`q=7.138*10^(-8)\ C`

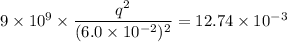
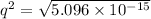
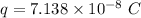
The time taken after charging beings is

`t=(q)/(C)`

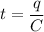
Put the value into the formula

`t=(7.138*10^(-8))/(7.0*10^(-9))`

`t=10.19\ sec`

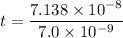
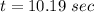
Hence, (a). The 2.0 g metal cube move fast than the 4 g metal cube.

(b). The time taken is 10.19 sec.