Answer: 0.00011323
Explanation:
Given : A multiple-choice examination has 15 questions, each with five possible answers, only one of which is correct.
i.e. Probability of getting a correct answer =
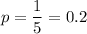
Using Binomial probability formula ,
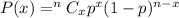
The probability that he answers at least ten questions correctly will be :-
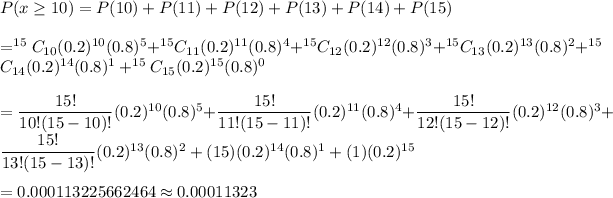
Hence, the probability that he answers at least ten questions correctly = 0.00011323