Question

A lead bullet with 30-g of mass traveling at 600 m/s hits a thin iron wall and emerges at a speed of 300 m/s. Suppose 50% of the heat generated is absorbed by the bullet, and the initial temperature of the bullet is 20°C. Find the final phase and temperature of the lead bullet after the impact. The specific heat of the liquid lead can be assumed to be the same as that of the solid lead.

Answer 1

liquid state of lead T = 547ºC

Step-by-step explanation:

The temperature change of the lead bullet can be found by the calorimetry equation

Q = m
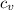`c_(v)` ΔT

Where heat is the energy transferred to lead during the crash, we can find average work

W = F x

With the crash it is very short we can use the average speed of the projectile during the crash

`v_(m)` = (
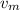`v_(f)` + v₀) / 2 = (600 + 300) / 2

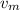`v_(m)` = 450 m / s

This speed of the projectile inside the wall is very inaccurate, but it is better than using any of the two speeds given (initial and final)

W = Δp vm

W = (m
`v_(f)` -m v₀) vm

W = m (
`v_(f)` -v₀) vm

W = 30 10⁻³ (300-600) 450

W = 4050 J

As we have a shock let's use the momentum

I = F t = ΔP

F = Δp / t

Let's replace

W = (Dp / t) x

With the crash it is very short we can use the average speed of the projectile during the crash

`v_(m)` = (
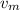`v_(f)` + v₀) / 2 = (600 + 300) / 2

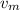`v_(m)` = 450 m / s

This speed of the projectile inside the wall is very inaccurate, but it is better than using any of the two speeds given (initial and final)

W = Δp vm

W = (m
`v_(f)` -m v₀) vm

W = m (
`v_(f)` -v₀) vm

W = 30 10⁻³ (300-600) 450

W = 4050 J

They tell us that 50% of the heat is absorbed by lead

Q = 50% W

Q = 2025 J

Let's calculate the temperature , the specific heat of lead is

cv = 128 J/kg ºC

Q = m
`c_(v)` Δt

ΔT = Q / m
`c_(v)`

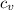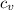
ΔT = 2025 / 3010⁻³ 128

`T_(f)`= 547C

If we review the periodic table, the melting point of lead is 327.3ºC and the boiling point is 1726ºC, since it has a higher temperature than the lead must be in a liquid state