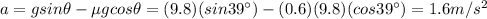Question

A 6.0 kg box slides down an inclined plane that makes an angle of 39° with the horizontal. If the coefficient of kinetic friction is 0.6, at what rate does the box accelerate down the slope? A 6.0 kg box slides down an inclined plane that makes an angle of 39° with the horizontal. If the coefficient of kinetic friction is 0.6, at what rate does the box accelerate down the slope?

(A) 2.1 m/s2
(B) 1.6 m/s2
(C) 1.9 m/s2
(D) 1.8 m/s2

Answer 1

(B) 1.6 m/s^2

Step-by-step explanation:

The equation of the forces acting on the box in the direction parallel to the slope is:

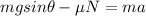`mg sin \theta - \mu N = ma` (1)

where

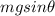`mg sin \theta` is the component of the weight parallel to the slope, with m = 6.0 kg being the mass of the box, g = 9.8 m/s^2 being the acceleration of gravity,
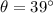`\theta=39^(\circ)` being the angle of the incline

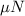`\mu N` is the frictional force, with
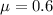`\mu = 0.6` being the coefficient of kinetic friction, N being the normal reaction of the plane

a is the acceleration

The equation of the force along the direction perpendicular to the slope is

`N-mg cos \theta =0`

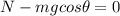
where
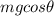`mg cos \theta` is the component of the weight in the direction perpendicular to the slope. Solving for N,

`N=mg cos \theta`

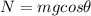
Substituting into (1), solving for a, we find the acceleration:

`a=gsin \theta- \mu g cos \theta=(9.8)(sin 39^(\circ))-(0.6)(9.8)(cos 39^(\circ))=1.6 m/s^2`