Question

A market researcher for a provider of music player accessories wants to know the proportion of customers who own cars to assess the market for a new car charger. A survey of 700 customers indicates that 76​% own cars.

​a) What is the estimated standard deviation of the sampling distribution of the​ proportion?
​b) How large would the estimated standard deviation have been if he had surveyed only 175 customers​ (assuming the proportion is about the​ same)?

Answer 1

Answer: a) 0.0161

b) 0.0323

Explanation:

The standard deviation of the sampling distribution of the​ proportion :

`\sigma_p=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

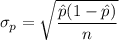
a ) Given : n=700 and
`\hat{p}=0.76`

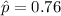
Then, the standard deviation of the sampling distribution of the​ proportion:

`\sigma_p=\sqrt{(0.76(1-0.76))/(700)}=0.0161422250192\approx0.0161`

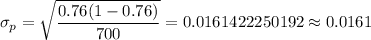
Hence, the estimated standard deviation of the sampling distribution of the​ proportion =0.0161

b) If n= 175 and
`\hat{p}=0.76`

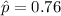
Then, the standard deviation of the sampling distribution of the​ proportion:

`\sigma_p=\sqrt{(0.76(1-0.76))/(175)}=0.0322844500385\approx0.0323`

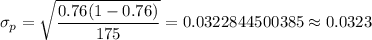
Hence, the estimated standard deviation have been if he had surveyed only 175 customers​= 0.0323