Question

Doppler shifted hydrogen absorption lines are seen in the spectrum of a star.

The hydrogen line at 656.28 nm is seen to be shifted to 656.08 nm.
How fast is the star moving (Note: The speed of light is approximately 300,000 km/s, or 3 × 105
km/s.)?
10)____
A) about 1,000 km/s
B) about 1,000,000 km/s
C) about 100 km/s
D) about 10,000 km/s

Answer 1

Step-by-step explanation:

It is given that,

Wavelength of hydrogen line,
`\lambda=656.28\ nm=656.28* 10^(-9)\ m`

Shift in wavelength,
`\lambda'=656.08\ nm=656.08* 10^(-9)\ m`

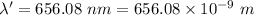
According to Relativistic Doppler Effect, the shift in wavelength is given by :

`(\lambda')/(\lambda)=\sqrt{(1+v/c)/(1-v/c)}`

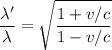
v is the speed of star

c is the speed of light

`((\lambda')/(\lambda))^2=(c+v)/(c-v)`

`v=c-(2c)/(((\lambda')/(\lambda))^2+1)`

`v=3* 10^8-(2* 3* 10^8)/(((656.08* 10^(-9))/(656.28* 10^(-9)))^2+1)`

`v=91438.32\ m/s`

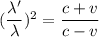
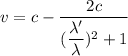
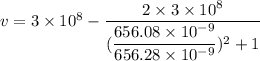
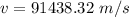
or

v = 91.43 km/s

So, the star is moving with a speed of about 100 km/s. Hence, this is the required solution.