Question

Q4. A fish processing company in Charlotteville processes three types of products: Type A,Type B and Type C.Its operations involve three basic activities: cleaning,cutting and packaging. Type A products require 4 minutes of cleaning 2 minutes of cutting and 2 minutes of packaging time.Type B products require 6 minutes of cleaning 4 minutes of cutting and 2 minutes of packaging time.Type C products require 8 minutes of cleaning 2 minutes of cutting and 4 minutes of packaging time.

Given that the total time available for cleaning,cutting and packaging is 3.5hours,2.5 hours and 1.5 hours respectively. a. Clearly defining your variables,show the model which represents the information given in this problem.State any restrictions on the variables in the problem.
Q5. Given that weekly demand curve of a local wine producer is p=50−0.1q, and that the total cost function is C(q)=1500+10q,where q bottles are produced each day and sold at a price of $p per unit.
a. Express the weekly profit as a function of price p. b. At what price must a bottle of wine be sold to realise this maximum profit? c. What is the maximum profit that can be made by the producer? Q6. A company is trying to expose as many people as possible to its new brand through social media advertising targeting 4 million possible viewers.A model for the number of people P,in millions,who are aware of the new brand after t days of advertising is estimated to be = 4(1 – −0.037) a. How many persons can they expect to meet in 1 week? b. How many days,to the nearest day,will the advertising campaign be launched that 60% of the possible viewers will be aware of the new brand?

Answer 1

Q4. Product types A , B , C ≥ = 0

Explanation:

Defining variables

let type A product = a

type B = b

type C = c

Model for the information

For cleaning, the total time is

4a + 6b + 8c = 3.5

For cutting, the total time is

2a + 4b + 2c = 2.5

For packaging, the total time is

2a + 2b + 4c = 1.5

The restrictions are

x , y , z >= 0

Q5.

Price per unit is defined as p=50−0.1q and revenue R(q)= qp(q)

R(q)= q(50-0.1q) Equation 1

R(q)= 50q−0.1q² Equation 2

The cost function as provided is

C(q)=1500+10q Equation 3

The profit function is given by

P(q)= R(q)- C(q) Equation 4 (a)

={50q−0.1q²} - {1500+10q}

=50q−0.1q² - 1500-10q

=40q−0.1q² - 1500 Equation 4(b)

Since we already have a price function as p=50−0.1q then multiplying each side by 10 and re-arranging and making q the subject we have

q=500-10p

Equation 4(b) can now be written while substituting q with 500-10p hence we obtain equation 5

40(500-10p)−0.1(500-10p)² - 150

20000-400p-0.1(250000-10000p+100p²)-1500

20000-400p-25000+1000p-10p²-1500

-6500+600p-10p² Equation 5

Therefore, the weekly profit is expressed as -10p²+600p-6500

b) Equation 5 is a parabolic equation which when compared with typical ax²+bx+c=0 hence in our case a=-10, b=600 and c=-6500 from equation 5

The maximum point is at
`((-b)/(2a) , (-d)/(4a) )`

Therefore, our
`(-b)/(2a) =(-600)/(2*-10) =30`

`(-d)/(4a)= (-b^2-4ac)/(4a)= (4ac- b^2)/(4a)= (4(-10)(-6500)- 600^2)/(4(-10))`

=
`(260000-360000)/(-40)`

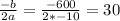
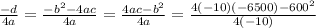
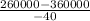
Therefore, our vertex is (30, 2500)

The price of a bottle to realize maximum profit is therefore $30

c)

As already shown in equations for part b, the maximum profit is $2500

Q6.

Since P is given as 4(1 – (Exp)-0.037t) then in one week t is 7 days for 1 week

hence P will be 4(1 – (Exp)-0.037*7)= 0.912 million

b)

The target is 4 million hence to get 60% means 60/100 of 4 million =2.4 million people

Substituting 2.4 where there's P our equation is

2.4= 4(1 – (Exp)-0.037t)

Dividing both sides of the above equation by 4 we obtain

0.6= (1 – (Exp)-0.037t)

Rearranging the above equation we obtain

(Exp)-0.037t= 1-0.6

(Exp)-0.037t= 0.4

t=24.76 days

t= 25 days the the nearest day

Keywords:

social media advertising targeting, advertising campaign, possible viewers, demand curve, Charlotteville