Answer:
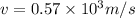
Mechanical energy is conserved in the presence of following forces:
a) electrostatic force
b) magnetic force
c) gravitational force
Step-by-step explanation:
Give data:
potential difference ,

we Know change in potential energy is given as
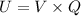
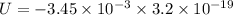
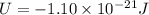
therefore, change in potential energy U is
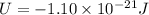
let speed of particle is v
from energy conservation theorem
loss of electrical PE = KE gained
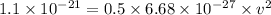
solving for v
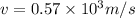
Mechanical energy is conserved for following forces:
a) electrostatic force
b) magnetic force
c) gravitational force