Answer: Our required probability is 2.8%.
Explanation:
Since we have given that
Probability of products slit with new blades have rough edges P(X) = 1%
Probability of products slit with blades of average sharpness exhibit roughness P(Y) = 3%
Probability of products slit with worn blades exhibit roughness P(Z) = 5%
Let A be the selected product that exhibit edge roughness.
P(A|X) = 25% = 0.25
P(A|Y) = 60% = 0.60
P(A|Z) = 15% = 0.15
So, the probability of products that exhibit edge roughness is given by
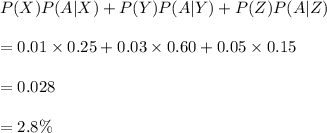
Hence, our required probability is 2.8%.