Question

An object is thrown upward from the top of a 160 foot building with an initial velocity of 48 feet per second. The height h of the object after t seconds is given by the quadratic equation h= 16t2+48t+160. When will the object hit the ground?

Answer 1

5 s

Step-by-step explanation:

when the object hits the ground, we're hitting the x-axis, where y = 0.

0 = -16t2 + 48t + 160

Let's divide -16 from both sides...

0 = t2 - 3t - 10

0 = (t - 5)(t + 2)

t - 5 = 0

t = 5 seconds

t + 2 = 0

t = -2

Unless we go back in time 2 seconds, this answer doesn't work.

The object will hit the ground in 5 seconds!

Answer 2

`t=5s`

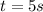
Step-by-step explanation:

From free falling objects we know that height is equal to:

`h=h_(o)+v_(oy)t+(1)/(2)gt^(2)`

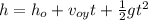
From the exercise we know that

`h_(o)=160ft\\v_(oy)=48ft/s\\g=-32 ft/s^(2)`

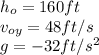
Being said that, we can calculate how long would it take to the object to hit the ground knowing that the height at that point is 0

`0=160ft+(48ft/s)t-(1)/(2)(32ft/s^2)t^2`

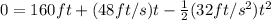
Solving the quadratic formula we got that

`t=\frac{-b±\sqrt{b^(2)-4ac}}{2a}`

`a=-16\\b=48\\c=160`

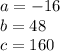
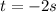`t=-2s` or
`t=5s`

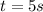
Since time can not be negative the logical answer is t=5s

So, the object hit the ground at 5s