Answer: a) 124,596, b) 2142691552.
Explanation:
Since we have given that
Number of distinguishable balls = 24
Number of boxes = 6
(a) In how many different ways can this be done?
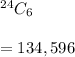
(b) In how many different ways can this be done if box 1 must get 12 balls, box 2 must get 7 balls, box 3 must get 5 balls, and boxes 4, 5, and 6 must be empty?
Number of ways would be

Hence, a) 124,596, b) 2142691552.