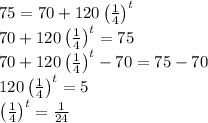Question

The temperature, H, in °F, of a cup of coffee t hours after it is set out to cool is given by the following equation. H = 70 + 120(1/4)t (a) What is the coffee's temperature initially (that is, at time t = 0)? 190 °F What is the coffee's temperature after 1 hour? 100 °F What is the coffee's temperature after 2 hours? (Round your answer to one decimal place.) 2 °F (b) How long does it take the coffee to cool down to 85°F? (Round your answer to three decimal places.) 5 hr How long does it take the coffee to cool down to 75°F? (Round your answer to three decimal places.) 5 hr

Answer 1

The temperature a t = 0 is 190 °F

The temperature a t = 1 is 100 °F

The temperature a t = 2 is 77.5 °F

It takes 1.5 hours to take the coffee to cool down to 85°F

It takes 2.293 hours to take the coffee to cool down to 75°F

Explanation:

We know that the temperature in °F, of a cup of coffee t hours after it is set out to cool is given by the following equation:

`H(t)=70+120((1)/(4))^t`

a) To find the temperature a t = 0 you need to replace the time in the equation:

`H(0)=70+120((1)/(4))^0\\H(0)=70+120\cdot 1\\H(0) = 70+120\\H(0)=190 \:\°F`

b) To find the temperature after 1 hour you need to:

`H(1)=70+120((1)/(4))^1\\H(1)=70+120((1)/(4))\\H(1) = 70+30\\H(1)=100 \:\°F`

c) To find the temperature after 2 hours you need to:

`H(2)=70+120((1)/(4))^2\\H(2)=70+120((1)/(16))\\H(2) = 70+(15)/(2) \\H(2)=77.5 \:\°F`

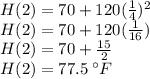
d) To find the time to take the coffee to cool down
`85 \:\°F`, you need to:

`85 = 70+120((1)/(4))^t\\70+120\left((1)/(4)\right)^t=85\\70+120\left((1)/(4)\right)^t-70=85-70\\120\left((1)/(4)\right)^t=15\\(120\left((1)/(4)\right)^t)/(120)=(15)/(120)\\\left((1)/(4)\right)^t=(1)/(8)`

`\mathrm{If\:}f\left(x\right)=g\left(x\right)\mathrm{,\:then\:}\ln \left(f\left(x\right)\right)=\ln \left(g\left(x\right)\right)`

`\ln \left(\left((1)/(4)\right)^t\right)=\ln \left((1)/(8)\right)`

`\mathrm{Apply\:log\:rule}=\log _a\left(x^b\right)=b\cdot \log _a\left(x\right)`

`t\ln \left((1)/(4)\right)=\ln \left((1)/(8)\right)`

`t=(\ln \left((1)/(8)\right))/(\ln \left((1)/(4)\right))\\t=(3)/(2) = 1.5 \:hours`

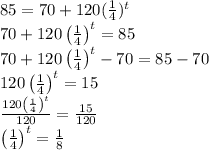
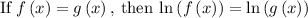
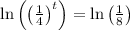
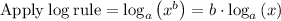
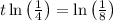
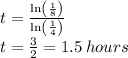
e) To find the time to take the coffee to cool down
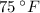`75 \:\°F`, you need to:

`75=70+120\left((1)/(4)\right)^t\\70+120\left((1)/(4)\right)^t=75\\70+120\left((1)/(4)\right)^t-70=75-70\\120\left((1)/(4)\right)^t=5\\\left((1)/(4)\right)^t=(1)/(24)`

`\ln \left(\left((1)/(4)\right)^t\right)=\ln \left((1)/(24)\right)\\t\ln \left((1)/(4)\right)=\ln \left((1)/(24)\right)\\t=(\ln \left(24\right))/(2\ln \left(2\right)) \approx = 2.293 \:hours`