Question

A professional driver drove a long linear route at an average speed of 30 miles per hour. Immediately after completing this drive, the driver turned around drove back on the same route at an average speed of 70 miles per hour. If the round trip took 2 hours, how many miles long is this route?

Answer 1

84 miles long is the route

Step-by-step explanation:

Let the distance is d

It is given that driver drove his car with 30 miles per hour

So time
`t=(d)/(30)`

And when he return his velocity is 70 miles per hour

So time

We know that average speed
`=(total\ distance)/(total\ time)=(2d)/((d)/(30)+(d)/(70))=42m/sec`

Total time of the trip is given as 2 hour

So total distance = total time × average speed = 42×2 = 84 miles

Answer 2

The route was 42 miles long.

Step-by-step explanation:

Let the distance covered from starting point to end point be x.

Average speed of the car = 30 mile/hour

Time taken to cover x distance = t

`t=(x)/(30 mile/hr)`

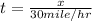
The distance covered from end point point to starting point back = x

Average speed of the car = 70 mile/hour

Time taken to cover x distance = t'

`t'=(x)/(70 mile/hr)`

Average speed of the car:

`(x+x)/(t+t')=(2x)/((x)/(30 mile/hr)+(x)/(70 mile/hr))=42 mile/hour`

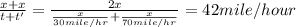
Total time taken in round trip = 2 hours

`\text{Average speed}=\frac{\text{Total distance}}{\text{Total time}}`

`42 mile/hr=\frac{\text{Total distance}}{2 hr}`

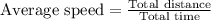
Total distance covered by car= 42 mile/hr × 2 hr = 84 miles

Distance of the route = 84 ÷ 2 = 42 mile