1 Answer

NETQuestion · Answer 1 · 2020-07-24T07:04:41+0000

An implication
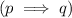$(p\implies q)$ is true if either the premise
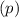(p) is false, or both the premise and conclusion
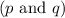$(p\text{ and }q)$ are both true, and false otherwise.

$\begin{array}cp&q&p\implies q&\\eg q&(p\implies q)\land\\eg q&\\eg p&(p\implies q)\land\\eg q\implies\\eg p\\T&T&T&&&&\\T&F&F&&&&\\F&T&T&&&&\\F&F&T&&&&\end{array}$

Negation
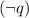$(\\eg q)$ is straightforward; if a statement is true, then its negation is false, and vice versa.

$\begin{array}cp&q&p\implies q&\\eg q&(p\implies q)\land\\eg q&\\eg p&(p\implies q)\land\\eg q\implies\\eg p\\T&T&T&F&&F\\T&F&F&T&&F\\F&T&T&F&&T\\F&F&T&T&&T\end{array}$

A conjunction
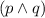$(p\land q)$ is true if both premises are true, and false otherwise.

$\begin{array}cp&q&p\implies q&\\eg q&(p\implies q)\land\\eg q&\\eg p&(p\implies q)\land\\eg q\implies\\eg p\\T&T&T&F&F&F\\T&F&F&T&F&F\\F&T&T&F&F&T\\F&F&T&T&T&T\end{array}$

Finally, by the rules of implication, we can fill the last column:

$\begin{array}cp&q&p\implies q&\\eg q&(p\implies q)\land\\eg q&\\eg p&(p\implies q)\land\\eg q\implies\\eg p\\T&T&T&F&F&F&T\\T&F&F&T&F&F&T\\F&T&T&F&F&T&T\\F&F&T&T&T&T&T\end{array}$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions