Question

Each time Henry visits the art museum he pays $15 for parking and $25 for admission. If he buys a membership for $110, parking will cost $10 and admission will be free. Choose the two equations that represent the situation. A. y = 110 + 10x; y = 40x B. y = 110 + 10x; y = 15x + 25 C. y = 110 + 10x; y = 25x + 15 D. y = 110x + 10; y = 40x Write an inequality that represents the number of museum visits for which the total member cost is less than the non-member cost. Use the inequality to find the smallest number of visits that satisfies the inequality y=110+10x;y=40x

Answer 1

Part 1) Option A. y = 110 + 10x; y = 40x

Part 2) The smallest number of visits is equal to 4

Explanation:

Part 1) Choose the two equations that represent the situation

Let

x ----> the number of museum visits

y ----> the total cost for the visit to the art museum

we know that

Non-member

`y=(15+25)x\\y=40x`

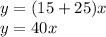
Member

`y=10x+110`

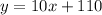
Part 2) Write an inequality that represents the number of museum visits for which the total member cost is less than the non-member cost

The inequality that represent the situation is

`10x+110 < 40x`

Solve for x

`110 < 40x-10x`

`110 < 30x`

`3.67 < x`

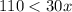
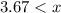
Rewrite

`x > 3.67\ visits`

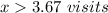
Round to the nearest whole number (Remember that the number of visits cannot be a decimal number)

therefore

The smallest number of visits is equal to 4