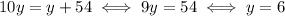5.
Let x be the age of the father and y be the age of the son. As of today, he's 3 times older, so we have
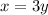
10 years ago their ages were, respectively, x-10 and y-10, and the father was 5 times older:
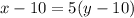
So, we have the system
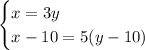
Using the first equation, we can substitute every occurrence of "x" with "3y" in the second equation:
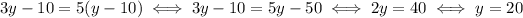
So, the son is 20 years old, which means that the father is 60 years old.
Indeed, 10 years ago they were 10 and 50 years old, so the father was 5 times older.
6.
Let x be the age of the grandfather and y the age of the granddaughter. We know that the grandfather is 10 times older:

He also is 54 years older:
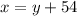
Again, if we substitute x=10y in the second equation we have