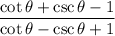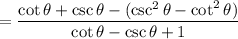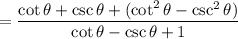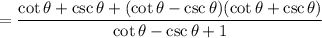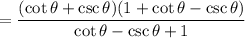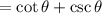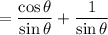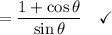25.
Show
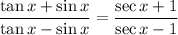
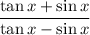
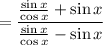
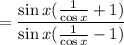
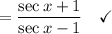
26.
Show
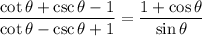
That's the cotangent half angle formula on the right, so I guess on the left too.
I fooled around with this one for a while before I took the hint which was to let
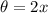 .
.
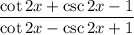
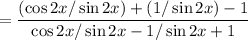
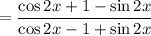
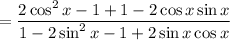
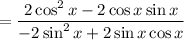
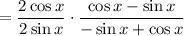
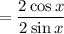
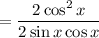
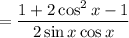
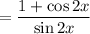
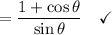
------
For another answer, let's use the hint on this one, which was to write
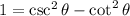
That's a good hint; first let's verify if it's true.
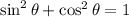
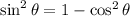
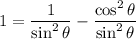

Now,