Arithmetic sequences have a common difference between consecutive terms.
Geometric sequences have a common ratio between consecutive terms.
Let's compute the differences and ratios between consecutive terms:
Differences:
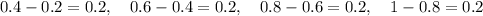
Ratios:
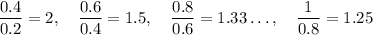
So, as you can see, the differences between consecutive terms are constant, whereas ratios vary.
So, this is an arithmetic sequence.