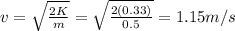Question

The spring is compressed a total of 3.0 cm, and used to set a 500 gram cart into motion. Find the speed of the cart at the instant it is released, assuming all the elastic potential energy is converted.

Answer 1

1.15 m/s

Step-by-step explanation:

Part of the question is missing. Found the missing part on google:

"1. A hanging mass of 1500 grams compresses a spring 2.0 cm. Find the spring constant in N/m."

Solution:

First of all, we need to find the spring constant. We can use Hooke's law:

`F=kx`

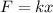
where

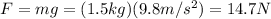`F=mg=(1.5 kg)(9.8 m/s^2)=14.7 N` is the force applied to the spring (the weight of the hanging mass)

x = 2.0 cm = 0.02 m is the compression of the spring

Solving for k, we find the spring constant:

`k=(F)/(x)=(14.7)/(0.02)=735 N/m`

In the second part of the problem, the spring is compressed by

x = 3.0 cm = 0.03 m

So the elastic potential energy of the spring is

`U=(1)/(2)kx^2=(1)/(2)(735)(0.03)^2=0.33 J`

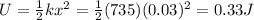
This energy is entirely converted into kinetic energy of the cart, which is:

`U=K=(1)/(2)mv^2`

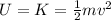
where

m = 500 g = 0.5 kg is the mass of the cart

v is its speed

Solving for v,

`v=\sqrt{(2K)/(m)}=\sqrt{(2(0.33))/(0.5)}=1.15 m/s`