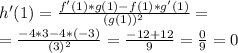Question

If f and g are differentiable functions for all real values of x such that f(1) = 4, g(1) = 3, f '(3) = −5, f '(1) = −4, g '(1) = −3, g '(3) = 2, then find h '(1) if h(x) = the quotient of f of x and g of x.

Answer 1

h '(1) = -24

gradppoint

Answer 2

h'(1)=0

Explanation:

We use the definition of the derivative of a quotient:

If
`h(x)=(f(x))/(g(x))`, then:

`h'(x)=(f'(x)*g(x)-f(x)*g'(x))/((g(x))^2)`

Since in our case we want the derivative of
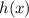`h(x)` at the point x = 1, which is indicated by: h'(1), we need to evaluate the previous expression at x = 1, that is:

`h'(1)=(f'(1)*g(1)-f(1)*g'(1))/((g(1))^2)`

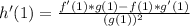
which, by replacing with the given numerical values:

`f(1) =4\\g(1)=3\\f'(1)=-4\\g'(1)=-3`

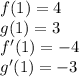
becomes:

`h'(1)=(f'(1)*g(1)-f(1)*g'(1))/((g(1))^2)=\\=(-4*3-4*(-3))/((3)^2)=(-12+12)/(9) =(0)/(9) =0`