Answer:
- The speed of the boat in still water is 8 miles per hour.
- The speed of the current is 4 miles per hour.
Solution:
We know the distance formula,
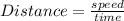
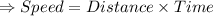
As boat travelled 240 miles downstream in 20 hours,
speed=
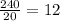 miles per hour.
miles per hour.
As boat travelled 240 miles upstream in 60 hours,
speed=
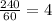 miles per hour.
miles per hour.
Let the speed of boat in still water be x and the speed of current be y.
So, the equations formed are:
 (downstream) --- (a) and
(downstream) --- (a) and
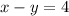 (upstream). --- (b)
(upstream). --- (b)
On solving, (a)
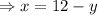 --- (c)
--- (c)
Substituting (c) in (b), we get

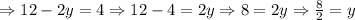
Therefore, y=4 --- (d)
On substituting (d) in (a) we get,

Therefore, x=8
Hence, Speed of boat in still water= 8 miles per hour and speed of current is 4 miles per hour.