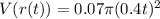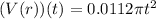Answer:
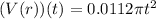
Explanation:
Given : An accident at an oil drilling platform is causing a circular-shaped oil slick to form. The volume of the oil slick is roughly given
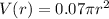 , where r is the radius of the slick in feet. In turn, the radius is increasing over time according to the function
, where r is the radius of the slick in feet. In turn, the radius is increasing over time according to the function
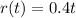 where t is measured in minutes.
where t is measured in minutes.
To find : (V of r)(t) and simply it ?
Solution :
Let
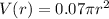 ....(1)
....(1)
and
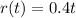 ....(2)
....(2)
For (V of r)(t)=V(r(t)) substitute equation (2) in (1),
i.e.