Question

The first tap can fill the pool in 10 hours. When the second tap was opened, the empty pool was filled in 6 hours. How long will it take the second tap to fill the pool alone?

Answer 1

15 hours

Explanation:

We can use the formula below to solve this:

`(t)/(x)+(t)/(y)=1`

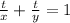
Where

t is the time taken for BOTH to fill up the pool [6 hours]

a is the time taken by first tap [10 hours]

b is the time taken by second tap [we need to find this]

Now putting in all the into and solving for y, we get:

`(t)/(x)+(t)/(y)=1\\(6)/(10)+(6)/(y)=1\\(6)/(y)=1-(6)/(10)\\(6)/(y)=(2)/(5)\\2y=30\\y=15`

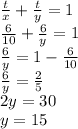
Hence, its gonna take 15 hours for the second tap to fill the pool alone.