Answer:
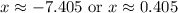
Explanation:
1. Set up the equation
Let x = the number. Then
7x = seven times the number and
x² = the square of the number
x² + 7x = seven times the number added to the square of the number
x² + 7x = 3
Subtract 3 from each side
x² + 7x - 3 = 0
2. Solve the quadratic equation
Use the quadratic formula: a = 1; b = 7; c = -3.
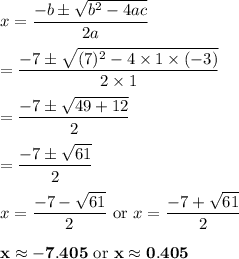
The graph of your quadratic crosses the x-axis at (-7.405,0) and (0.405,0).