Question

Complete the statements.

Answer 1

• Graph B has one real root.
• Graph A has a negative discriminant
• Graph C has an equation with the coefficients a=1, b=4, c=-2.

Explanation:

The number of real roots is the number of places where the graph intersects the x-axis. When the discriminant is negative, there are none. Graph A does not cross the x-axis, so has a negative discriminant.

Graph B intersects the x-axis at one point, so it has one real root.

Graph C has two real roots, consistent with the positive discriminant associated with the given coefficients:

`d=b^2-4ac=4^2-4(1)(-2)=16+8=24`

_____

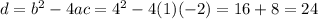
For quadratic ...

`y=ax^2+bx+c`

the discriminant is ...

`d=b^2-4ac`

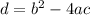
and the roots are ...

`x=(-b\pm√(d))/(2a)`

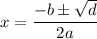
Then the roots are only real when the discriminant is non-negative. The square root function will not give real values for a negative argument.