Answer:
See explanation
Explanation:
Paul has three cube-shaped boxes. Each box is a different size and they are stacked from the largest to the smallest. Some information about the boxes is given below.
- The combined volume of the three boxes is 1,197 cubic inches.
- The area of one face of the medium box is 49 square inches.
- The volume of the smallest box is 218 cubic inches less than the volume of the medium box.
1. The medium box has the area of one face of 49 square inches, then
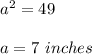
is the side length.
The volume of the medium box is

2. The volume of the smallest box is 218 cubic inches less than the volume of the medium box, then the volume of the smallest box is

Ib is the side length, then

The area of one face is
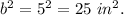
3. The volume of the largest box is
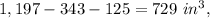
then if c is the side length,

4. The total height of the stack is the sum of all sides lengths:
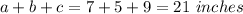
5. Find the surface area of each box:
In total, Paul needs
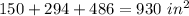
of wrapping paper. He has 1,000 square inches, so Paul has enough paper to wrap all 3 boxes.