Answer:
The production level will yield a maximum revenue when production level is approximately equal to 75,000.
Explanation:
Revenue is given by
R(x) =
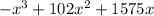
First, we differentiate R(x) with respect to x, to get,
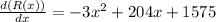
Equating the first derivative to zero, we get,
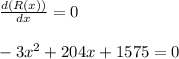
Solving, with the help of quadratic formula, we get,
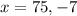
Again differentiation R(x), with respect to x, we get,
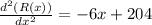
At x = 75
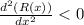
Thus, maxima occurs at x = 75 for R(x).
Thus, the production level will yield a maximum revenue when production level is approximately equal to 75,000.