Question

Three times as many children as adults attended a concert on Saturday. An adult ticket cost $7 and a child’s ticket cost $3. The theatre collected a total of $6000. How many people bought tickets?

Answer 1

For this case we propose a system of equations:

x: Let the variable representing the number of children in the concert

y: Let the variable representing the number of adults at the concert

According to the assistance we have:

`x = 3y`

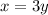
According to the cost we have:

`3x + 7y = 6000`

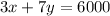
Substituting the first in the second equation we have:

`3 (3y) + 7y = 6000\\9y + 7y = 6000\\16y = 6000\\y = \frac {6000} {16}\\y = 375`

Thus, the concert was 375 adults.

On the other hand we have:

`x = 3 (375) = 1125`

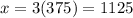
Thus, the concert was 1125 children.

In total they were:

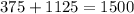`375 + 1125 = 1500` people

ANswer:

The concert was 1500 people