Answer:
The system of equations has no solution
Explanation:
The method of substitution consists in solving one equation for a variable and replacing it in the other equation.
In this case one of the equations is already solved for one of the variables (
 ):
):

So the next step is to plug this in the other equation wich is:
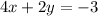
So we will have
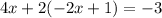
solving the parenthesis:

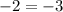
wich is not a valid answer, so the system of equations has no solution.