Question

Motorola used the normal distribution to determine the probability of defects and the number of defects expected in a production process. Assume

a production process produces items with a mean weight of 14 ounces.
a. The process standard deviation is 0.10 ounces, and the process control is set at plus or minus 1.75 standard deviations. Units with weights less
than 13.825 or greater than 14.175 ounces will be classified as defects. What is the probability of a defect (to 4 decimals)?
In a production run of 1000 parts, how many defects would be found (round to the nearest whole number)?​

Answer 1

a) 0.0801

b) 80

Explanation:

The z-score for 13.825 is

`Z=(13.825-14)/(0.10) =-1.75`

The probability of producing a unit with weight less than 13.825 is

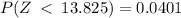`P(Z\:<\:13.825)=0.0401` ( Standard normal distribution table)

The z-score for 14.175 is

`Z=(14.175-14)/(0.10) =1.75`

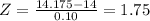
The probability of producing a unit with weight greater than 14.175 is

`P(Z\:>\:14.175)=0.0401`

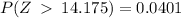
The probability of defect is

`P(Z\:<\:13.825)+P(Z\:>\:14.175)=0.0401+0.0401=0.0802`

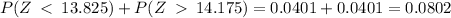
In a production run of 1000 parts, the expected number of defects is

`0.0802*1000=80.2`

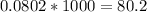
To the nearest whole number 80 defects will be found