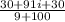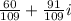Question

If x=(10-3i) and y=(3-10i), then xy=? and x/y=?

Answer 1

`xy=-109i`

`(x)/(y)=(60)/(109)+(91)/(109)i`

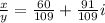
Explanation:

`xy=(10-3i)(3-10i)`

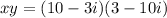
To compute x times y must use foil on the right hand side.

First:
`10(3)=30`

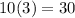
Outer:
`10(-10i)=-100i`

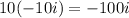
Inner:
`-3i(3)=-9i`

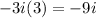
Last:
`-3i(-10i)=30i^2=-30`

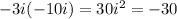
------------------------------------Add like terms:

`-109i`

----------------

`(x)/(y)`

`(10-3i)/(3-10i)`

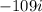
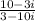
Multiply top and bottom by bottom's conjugate:

`((10-3i)(3+10i))/((3-10i)(3+10i))`

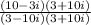
Foil the top and just do first and last of Foil for the bottom since the bottom contains multiplying conjugates:

`(30+100i-9i-30i^2)/(9-100i^2)`

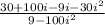
Replace
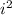`i^2` with -1:

`(30+91i+30)/(9+100)`

`(60+91i)/(109)`

`(60)/(109)+(91)/(109)i`