The rocket should be fired for 129600 seconds.
Why?
We can calculate for how long should the rocket be fired by using the following equation:
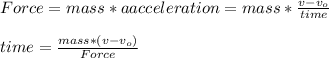
From the statement we know:
- Initial speed equal to zero.
- Force equal to 272N.
- Final speed (for the moment) equal to 62 m/s.
- Mass equal to 72000 Kg.
So, substituting and calculating, we have:
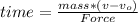
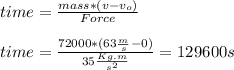
Hence, we have:
Variables: Time
Equations:
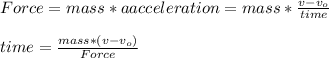
Answers: The rocket should be fired for 129600 seconds.
Have a nice day!