Answer:
Answer D: 8.7 cm
Explanation:
First compare the actual diameters of both cables to find out which one is larger. If we write both diameters in fraction form (as they are given), we need to have them expressed with the same denominator for a straight forward comparison:
Bundle A:
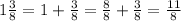
Bundle B:
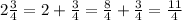
So we multiply this last fraction by 2 in numerator and denominator to obtain the same denominator as for Bundle A without actually changing its numerical value:
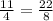
So now we compare Bundle A with bundle B, and see that bundle B has the larger diameter: 22/8 inches
The hole has to be 25% larger than this larger diameter, so we estimate 25% of 22/8 in is:
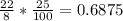 inches
inches
Therefore, the hole must be of diameter 22/8 in plus 0.6875 in = 3.4375 in
Now we convert this value into centimeters by multiplying it by 2.54 (since one inch is 2.54 cm):
3.4375 * 2.54 = 8.73125 cm
which rounded to the nearest tenth as requested in the problem is: 8.7 cm