Answer:
Option A)
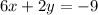
Explanation:
We are given the following information in the question:
x-intercept =
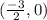
y-intercept =
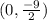
x-intercept is the value when y = 0 and the curve passes through the x-axis and y-intercept is the value when x = 0 and the curve passes through the y-axis.
Option A)

Hece, option A) is the correct required line.