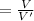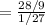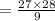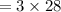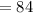Question

The dimensions of a rectangular prism are shown below. Length 1 1/3 feet Width 1 foot length 2 1/3 feet. The lengths of the sides of a small cube are 1/3 foot each. How many small cubes can be packed in the rectangular prism?

Answer 1

84 cubes

Explanation:

Given,

The dimension of the rectangular prism are,

`1(1)/(3)\text{ ft }* 1\text{ ft }* 2(1)/(3)\text{ ft }`

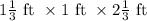
Hence, the volume of the prism,

`V=1(1)/(3)* 1* 2(1)/(3)`

`=(4)/(3)* (7)/(3)`

`=(28)/(9)\text{ cube ft}`

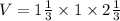
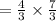
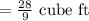
Now, the volume of a cube = side³,

If side =
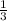`(1)/(3)` ft,

Then the volume of each cube,

`V'=((1)/(3))^3=(1)/(27)\text{ cube ft}`

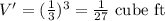
Hence, the number of cubes that can be packet in the prism

`=(V)/(V')`

`=(28/9)/(1/27)`

`=(27* 28)/(9)`

`=3* 28`

`=84`