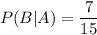Answer: D)
Explanation:
Given : A wallet contains 4 dimes, 5 pennies, and 7 nickels.
Total coins = 4+5+7=16
Event A is defined as drawing a dime on the first draw and event B is defined as drawing a nickel on the second draw.
After 1st coin draws as dime , the total coins left = 16-1=15
Total nickels left as same as before.
Now,
Probability of drawing 2nd coin a nickel given that 1st one was a dime:
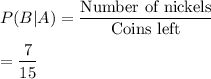
Hence,