Question

A coffee-cup calorimeter is used to determine the heat of reaction for the reaction of compound A with compound B. A(aq) + B(aq) → C(aq) When we add 16.10 mL of 0.189 M A at 23.722°C to 16.10 mL of 0.189 M B already in the calorimeter at the same temperature, the resulting temperature is observed to be 33.637°C. The heat capacity of the calorimeter has previously been determined to be 30.7 J/°C. Assume that the specific heat of the mixture is the same as that of water, 4.184 J/g·°C, and that the density of the mixture is 1.00 g/mL. How much heat, in joules, was released by the reaction? (Here we're looking for the magnitude of the heat. Your answer should be positive.)

Answer 1

`\rm 1.64* 10^(3)\; J`.

Step-by-step explanation:

Assume that his calorimeter is sufficiently effective, such that no heat had escaped to the surroundings. Heat from this solution would be absorbed by either

• the solution, or
• the coffee cup.

Temperature change:
`33.637 - 23.722 = \rm 9.915\; ^\circ C`.

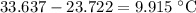Heat absorbed by the solution:

Only the specific heat capacity (per unit mass) of the solution is given. Both the mass of the solution and the temperature change will be required for determining the energy change. Start by finding the mass of the solution.

`m = \rho \cdot V = 2* 16.10 * 1.00 = \rm 32.10\; g`.

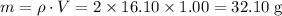Calculate the amount of heat absorbed from the specific heat:

`Q = c\cdot m \cdot \Delta T = 4.814* 32.10 * 9.915 = \rm 1335.80\; J`.

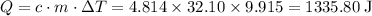Heat absorbed by the coffee cup:

The heat capacity of the coffee cup is given. Only the temperature change will be required for finding the amount of heat absorbed.

`Q = C\cdot \Delta T = \rm 30.7* 9.915 = 304.391\; J`.

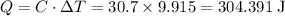Heat that this reaction produces

Find the sum of the two parts of heat. Round to three significant figures as in the heat capacity of the coffee cup and the density of the solution.

`\rm 1335.80+ 304.391 = 1.64* 10^(3)\; J`.