Answer:
a:
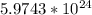
b:

Explanation:
For a:
The combined mass is the totaled mass of all the objects.
So that would be
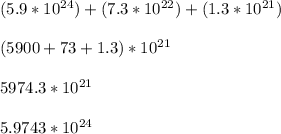
For b:
We need to find how many of the moon-Earth-Pluto combinations are needed to match the mass of the sun.
So, we would calculate the following:
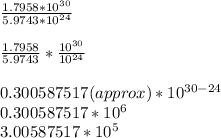
So it would take approximately
 of the moon-Earth-Pluto combos to match the mass of the sun.
of the moon-Earth-Pluto combos to match the mass of the sun.