Question

A rectangular field is 95 meters long and 65 meters wide. Give the length and width of another rectangular field that has the same perimeter but a smaller area.

Answer 1

There are a ton of answers. For instance, 1m by 159m.

Explanation:

The formula for the area is
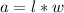`a=l*w`, where
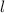`l` and
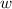`w` are constants.

The formula for perimeter is
`p=2l+2w`

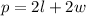
The question wants another rectangle that has the same perimeter, but a smaller area.

The perimeter of the two fields has to be:

`p=(2*95)+(2*65)\\p=190+130\\p=320`

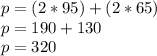
Thankfully, the question never specified how much smaller the area has to be. So let's go to the logical extreme and make it 1 meter wide. To conserve the perimeter, we'd have to add the removed 64 meters to the original 95 meters of length, resulting in a rectangle with a width of 1m and a length of 159m. This results in an area of exactly 159
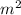`m^(2)`. The original rectangle had an area of 6175
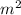`m^(2)`. Mission accomplished!

But why stop there? Let's go even further down this rabbit hole!

Instead of 1, why don't we take it several steps further and use 0.0000001? At that point, the length would end up being 159.9999999m.

The area would be 0.00001599999999
`m^(2)`.

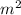Let's go further!!

Width: 0.00000000000000000001

Length: 159.99999999999999999999

Area: 0.00000000000000000001599999999999999999999 (approximate).

One more, for old time's sake.

Width: 0.00000000000000000000000000000000000000000000000001m

Length: 159.99999999999999999999999999999999999999999999999999m

Area: 0.00000000000000000000000000000000000000000000000015999999999999999999999999999999999999999999999999999
`m^(2)`

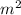
At that point, there's so little area in the plot of land that you could claim it has no area!