Question

Astronomers treat the number of stars in a given volume of space as a Poisson random variable. The density in the Milky Way Galaxy in the vicinity of our solar system is 1 star per 16 cubic light years. (a) What is the probability of 2 or more stars in 16 cubic light years? Probability = . [Round your answer to three decimal places (e.g. 98.765).] (b) How many cubic light years of space must be studied so that the probability of 1 or more stars exceeds 0.98? cubic light years of space. [Round your answer to the nearest integer.]

Answer 1

a) 0.264 b) 64 cubic light years

Explanation:

Let be X the following event : ''Number of stars in a given volume of space''

X~Poisson variable

X~P(k;λ)

The density is 1 star per 16 cubic light years so

λ = 1 star / 16 cubic light years

The probability mass function of X is :

f(x)= P(X = k) = {[(λt) ^ k].[(e) ^ (-λt)]} / k! ; k∈Νo

We measure t in units of 16 cubic light years

λt = (1 star / 16 cubic light years).(1).(16 cubic light years) = 1 star

a)

`P(X\geq 2)= 1-P(X<2)=1-P(X=0)-P(X=1)`

`P(X\geq 2)=1-f(0)-f(1)`

`P(X\geq 2) = 1-e^(-1)-e^(-1) =0.264`

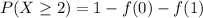
b) We are looking for t so that :

`P(X\geq1)\geq 0.98\\1-P(X<1)\geq 0.98\\1-f(0)\geq 0.98\\1-e^(-t) \geq 0.98\\-e^(-t) \geq -0.02`

`e^(-t) \leq 0.02\\ln(e^(-t)) \leq ln(0.02)\\-t\leq ln(0.02)\\t\geq -ln(0.02)\\t\geq 3.912`

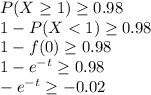
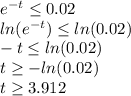
t≥3.912 ≈4

We should explore 4.16= 64 cubic light years of space to find a star with the certain of 98%.