Answer:
a) 38.8224 knots
b) 86° due north of east
c) 4.63 h
d) 86° due south of east
Step-by-step explanation:
The velocity of B relative to A:
![V_(A/B)=V_A-V_B =[-21*cos(45),21*sin(45)]-]-25*sin(45),-25*cos(45)]](https://img.qammunity.org/2020/formulas/physics/college/z7k393grwxm41xcmskmvsmtvpx3e4trnun.png)
![V_(A/B)=[2.7539,38.7246]knots/h](https://img.qammunity.org/2020/formulas/physics/college/wxlq4y7nei1mluhdfpoyk4qa1b95gjp8e7.png)
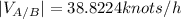
For the angle: It's on the first quadrant, so:
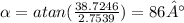
For the amount of time, we will use the relative velocity calculated:
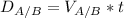
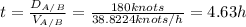
The bearing of B relative to A will have the opposite direction of A relative to B, so:
α = -86° This is 86° due south of east