Answer:
the net present value at a rate r = 9% is $91,0.2.61478
Step-by-step explanation:
From data given the initial investment calculated as
The initial investment is
17,000,000-5,000,000 = 12,000,000
Hence at year 0, the company has a cash flow of
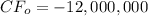
And for the next 15 years the cash flows are:
CF_i= 1,500, 000 for i 1, 2, .., 15
Hence the net present value at a rate r = 9% is:
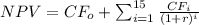
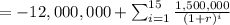
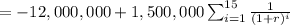
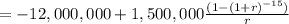
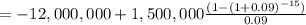
= 91,0.2.61478
Since NPV >0 then they should purchase the new engines.
They should purchase the new engines because it would result in a rate of return
greater than the rate of 9% of the other investment.