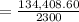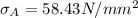Answer:
Step-by-step explanation:
Given data:
length of Steel bolt
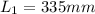
Length of aluminium cylinder

Pitch of bolt p = 1mm
Modulus of elasticity of steel E = 215 GPa
Modulus of elasticity of aluminium = 74 GP
Area of bolt
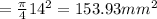
Area of cylinder = 2300 mm^2
n =1
By equilibrium
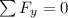
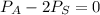
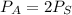
By the compatibility
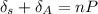
Displacement in steel is
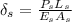
Displacement in Aluminium is
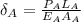
from compatibility equation we have
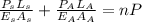
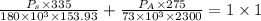

substitute
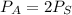
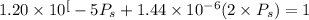
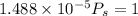
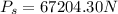
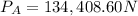
Stress in Aluminium