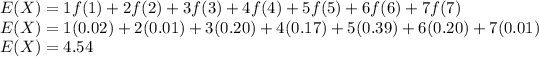Question

Consider randomly selecting a student who is among the 14,000 registered for the current semester in a college. Let be the number of courses the selected student is taking, and suppose that has the following probability distribution: 1 2 3 4 5 6 7 0.02 0.01 0.20 0.17 0.39 0.20 0.01 Find the expected number of courses a student is taking in this semester (write it up to second decimal place).

Answer 1

`E(X)=4.54`

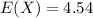
Explanation:

Let be X the event : ''The number of courses the selected student is taking''

X is a discrete random variable.

X has the following probability function :

`f(1)=0.02\\f(2)=0.01\\f(3)=0.20\\f(4)=0.17\\f(5)=0.39\\f(6)=0.20\\f7)=0.01`

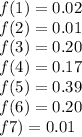
Let's check that f(x) is a probability function :

The sumatory of all it ranges must be equal to 1

`f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)=1\\0.02+0.01+0.20+0.17+0.39+0.20+0.01=1\\1=1`

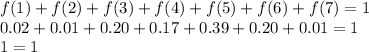
Then f(x) defines a probability function.

The expected number of the random variable X is :

The sum of all its xi.f(xi) from i = 1 to n

`E(X) = 1f(1)+2f(2)+3f(3)+4f(4)+5f(5)+6f(6)+7f(7)\\E(X)=1(0.02)+2(0.01)+3(0.20)+4(0.17)+5(0.39)+6(0.20)+7(0.01)\\E(X)=4.54`